This section covers the Kalman Filter Algorithm. First we'll cover the State Space format of modeling and measuring a discrete-time dynamic system of estimated states, noisy inputs, and noisy measurements. Second, we'll explore all the different pieces of information about our system necessary to inform the algorithm. Third, the specific Kalman Filter Algorithm constructed based off of those parameters. Finally, we'll use some example state spaces and measurements to see how well we track.

Note: all images below have been created with simple Matlab Scripts. If seeing the code helps clarify what's going on, the .m files can all be found under internal location cs:localization:kalman.

The State Space Format is a universally standardized format for dynamic systems in the signals and controls community. In the continuous-time domain, the derivative of the state $\dot{x}(t)$ is a linear function of $x(t)$. In the discrete-time domain, where we'll be operating, the next state $x[k+1]$ is a linear function of the current state $x[k]$.

$$ X_{k+1} = AX_k + B(u_k + \sim\mathcal{N}(0,Q^2)) \\ Y_k = CX_k + \sim\mathcal{N}(0,\sigma_m^2) $$

Vector $X_k$ is the State Vector which contains all states of the system at time-step $k$. These include things like position, velocity, orientation, voltage, etc. Matrix $A$ is the Transmission Matrix, which contains the dynamics of the system, and calculates the next state given the current state. $B$ is the input matrix, which describes the dynamics of inputs $u$.

Vector $Q$ is the Process Noise of the system, which is the combination of the variance of the inputs $\sigma_u^2$ and an estimated degree of possible external forces $\sigma_{ext}^2$. $Q^2 = \sigma_u^2 + \sigma_{ext}^2$ Random forces from bumping into walls, random currents in the water, diver interaction, and other unpredictable perturbations. Put another way, $Q$ describes the uncertainty involved when predicting into to future, even given perfect information about the present State. Were there no external forces, perfect actuators, and a perfect initial state $x_0$, the system state could be predicted perfectly into the future. This is obviously not the case in the real world, hence the need to specify uncertainty in the model, and thus in predicting the future states.

Vector $Y_k$ is the measurement vector. It contains the values taken from the sensors. Matrix $C$ is the Emission Matrix, which describes the linear function that relates the system state to the measurement values. $\sigma_m$ is the noise vector which describes how noisy each individual sensor measurement is.

The Kalman Filter is a two-stage process of prediction and measurement. First, based on the previous state estimate $\hat{X}_{k-1}$ and inputs $u_{k-1}$, an initial current state estimate $\hat{X}_{k'}$ is predicted. The confidence of the Previous Estimate is contained in the Covariance Matrix $P$ From this estimate, a further estimate $\hat{Y}_k$ of what the sensors should be reading given $\hat{X}_{k'}$ is calculated using the Emission Matrix $C$.

Second, the true, noisy measurements $Y_k$ are received and compared with the expected sensor values $\hat{Y}_k$. A compromise between the noisy measurements and the expected measurement is arrived at based upon the noise of the sensors $\sigma_m$ and the uncertainty of the measurement predictions calculated from $P$. This compromise is encapsulated in a value $\hat{K}$ terms the 'Kalman Gain'. The official $\hat{X}_{k}$ is then calculated from the Emission Matrix $C$ and the compromise of sensor values. The estimate of our state for this time step is made, and the process repeats to estimate the state $X_{k+1}$ at the next time step.

$$ \hat{X}_{k'} = A\hat{X}_{k-1} + Bu_{k-1}, \qquad P_{k'} = AP_{k-1}A' + Bdiag(Q^2)B' \\ \hat{K} = P_{k'}C'/(CPC'+diag(\sigma_m^2)) \\ \hat{X}_k = \hat{X}_{k'} + \hat{K}(Y_k - C\hat{X}_{k'}),\qquad P_k = (I_{n} - \hat{K}C)P_{k'} $$

<inline code example to be explicit>

The above update loop requires initialization. Each execution of the loop relies on the model itself, and values from the previous loop. Upon start-up, any program must first build the model. To do so, we must construct our state vector $X$, construct our Transition Matrix $A$ and Input Matrix $B$ that describe the physical dynamics of the system, and construct an emission matrix $C$ that ties our measured sensor values $Y$ to be functions of the state $X$. As you will likely be changing the number of sensors and motors, as the submarine is tinkered with and modules are added, removed, or temporarily disabled, it is advisable to make this a dynamic process that takes information from a calibration file and constructs the $B$ and $C$ matrices.

Process Noise $Q$ and sensor noise $\sigma_m$ must be estimated. $Q$ should likely be loaded from a calibration file, and $\sigma_m$ dynamically created alongside $C$ with information from such a file.

Once the model is created, initial parameters must be selected. A good default is to set your state estimate $\hat{X}_0$ to be all zeros, or their equivalent. For instance, if the 9 elements of the 3×3 orientation matrix are part of your state, they would be set as an identity matrix $I_3$. This initial guess at our state is accompanied by a the covariance matrix $P_0$ being a diagonal matrix of very large numbers. This will ensure that all predictions of the estimated state from the model are ignored in the face of any sensor measurement that might have some semblance of an idea of what the state is. The model should still begin to produce reliable results and be taken seriously in a short number of time steps, as even after a single measurement, the state estimate $\hat{X}$ has a better (smaller) variance than any sensor measurement, and raw sensor measurements typically are pretty good on their own.

Finally, calibration values must be estimated or directly measured and stored upon start-up. Things like the specific orientation and magnitude of the local magnetic field, the magnitude of gravity (direction is always tautologically 'down' along the z axis), and the drift of individual gyroscopes. These parameters, among others, are vital to the utilization of your sensor data to estimate the world, and are liable to change with location or time. Often times calculating these parameters require specific manipulation of the submarine - such as keeping the submarine perfectly still for measuring gyroscopic drift - and should potentially be made part of an executable calibration-script to be run at the push of a button once the submarine is appropriately staged.

Other sections will elaborate on how to build these matrices and perform these calibrations. Below is a simple example of a kalman filter code - the mechanics themselves are quite simple to set up.

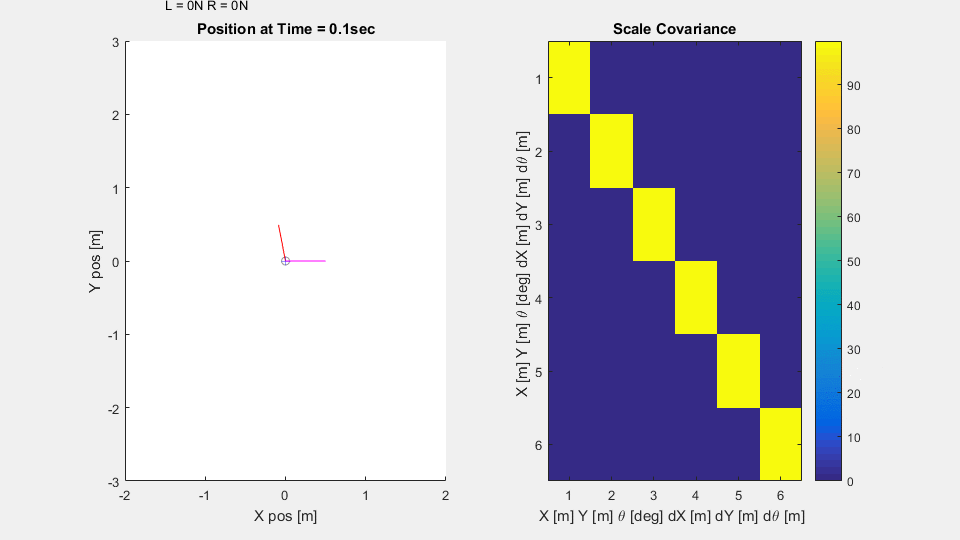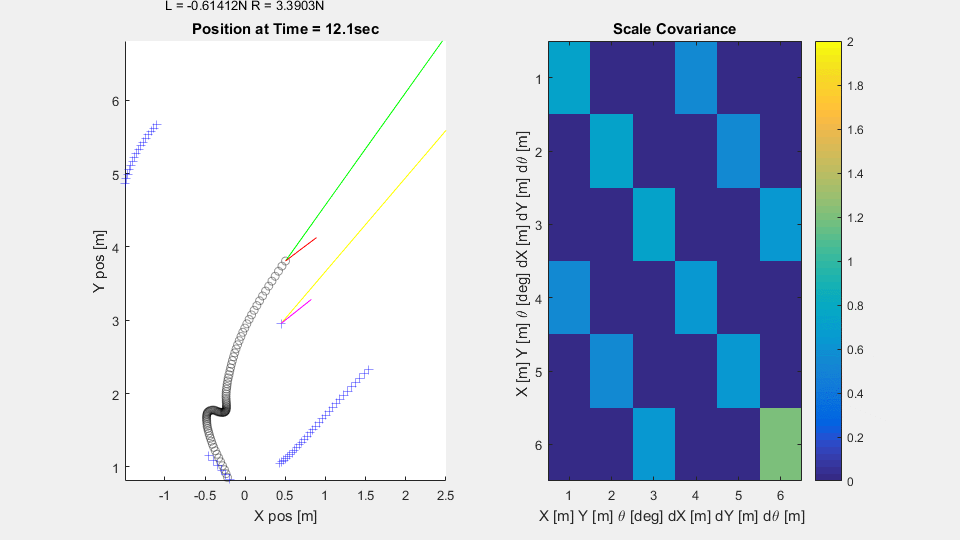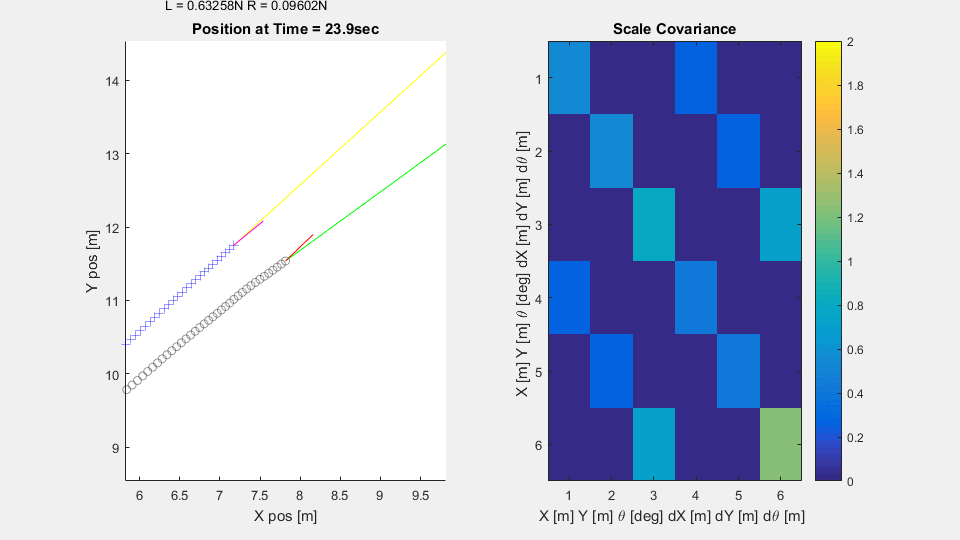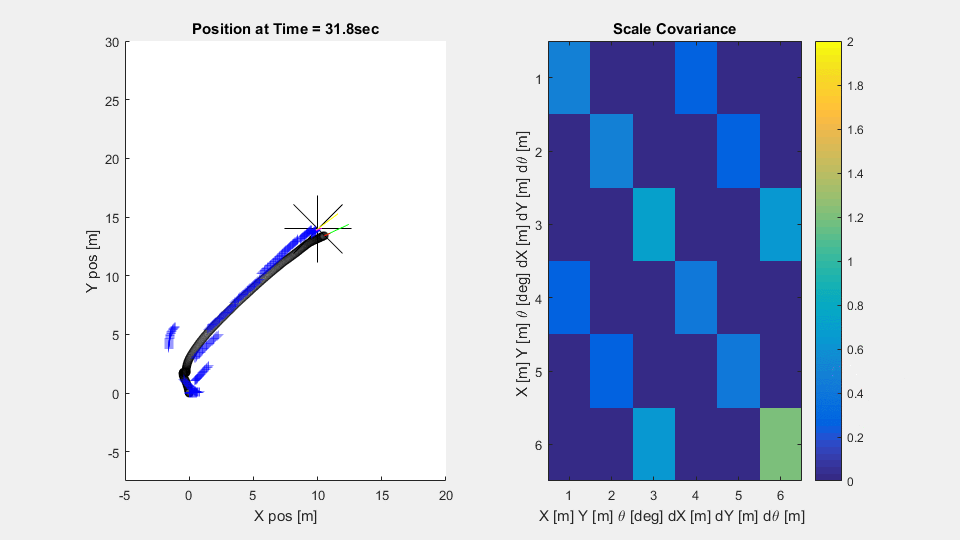
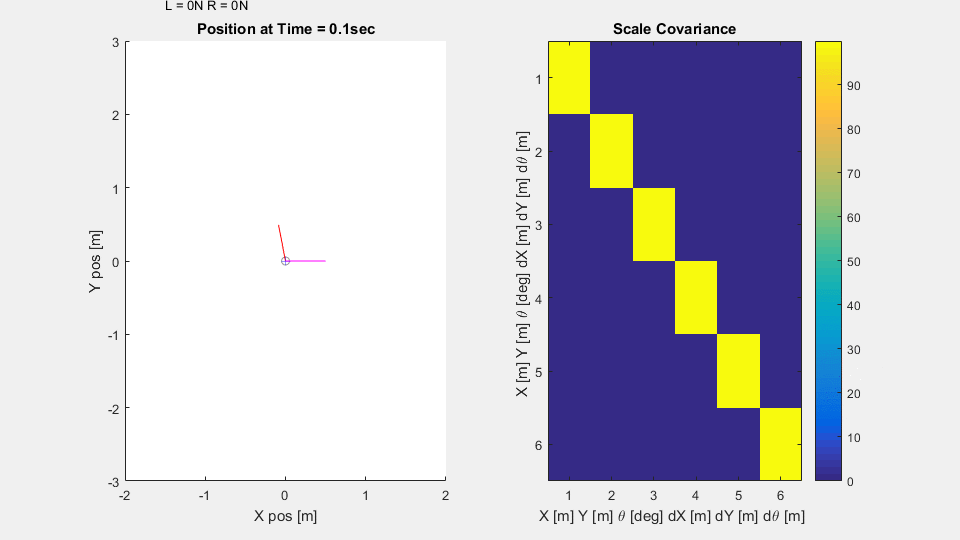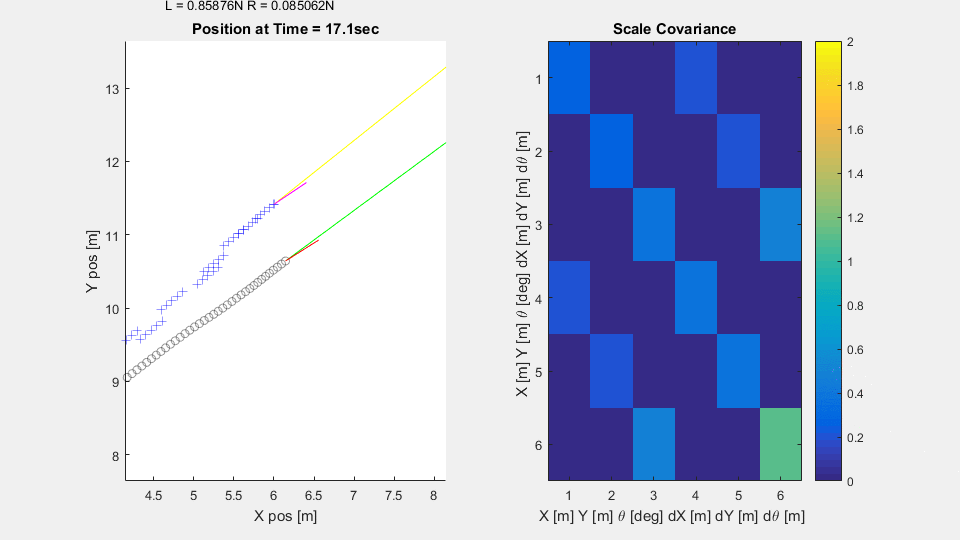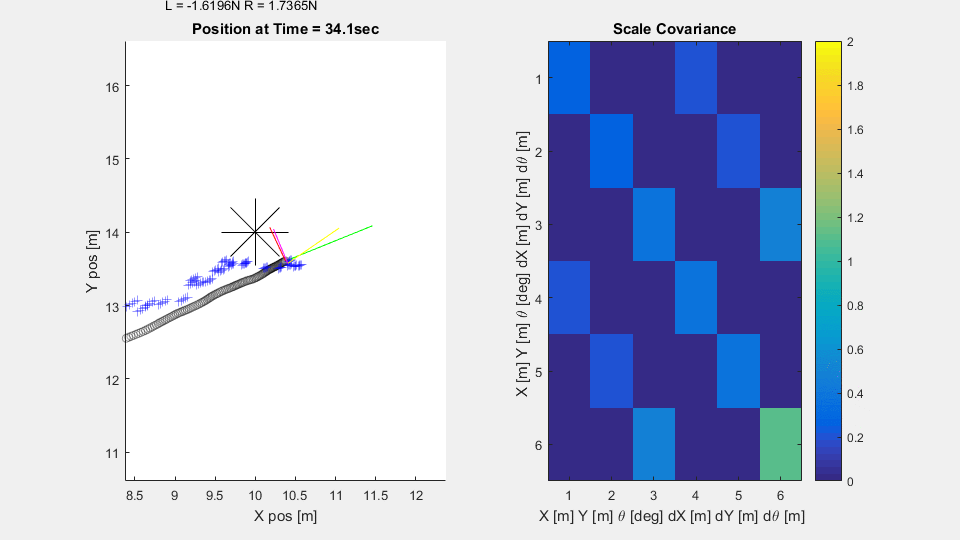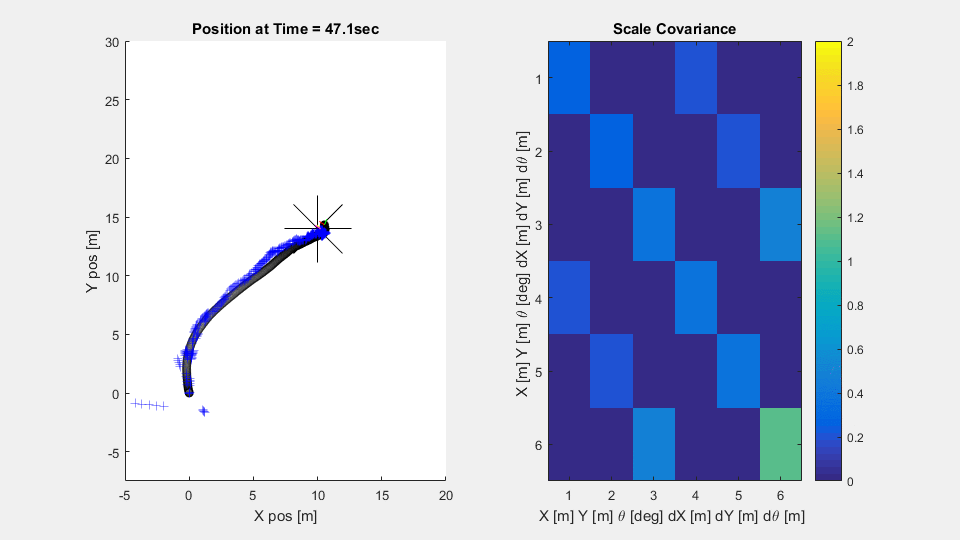
In the simulation, the vehicle on the 2D plane has thrusters to let it control orientation and forward motion. The process noise in the system is relatively low, but the sensors are noisy and ping less frequently. From a constant starting point and random orientation, the submarine attempts to reach its target, meandering less as it becomes more confident in its knowledge of the world.

The Scaled Covariance axes is a heatmap of the covariance matrix $P$ scaled by the standard deviations $\sigma_x, \sigma_y,$ and $\sigma_\theta$ of each of the sensors. The derivative values $\dot{x}, \dot{y},$ and $\dot{\theta}$ are scaled by $\frac{\sigma_x}{dt}, \frac{\sigma_y}{dt},$ and $\frac{\sigma_\theta}{dt}$ Note how the variances along the diagonal mostly drop below unity - suggesting the submarine is more confident in it's state estimation $\hat{X}$ than any individual sensor reading. Note also that the variances are all lower when the sensors are reporting in more frequently. Finally note how the variances are all lower when the submarine is moving quickly. Disagreements between expected and measured position become much more significant when projected into the future with a high velocity.

With sensor reporting at every 3 seconds:

With sensor reporting at every 0.5 seconds:

Unfortunately the code looks more complicated than what's above, because I through orientation into the mix, which adds a bit of complexity, and a control system necessary to make the little figure behave appropriately. However, the parameters set should all look very familiar, as should the Kalman Update Process. The Modeling code is normally handled by… well… reality. And the Control System producing the inputs from your sensor measurement estimates is some other poor shmuck.

Here we initialize all the matrices we'll need for our model. $A$ Transition Matrix, $B$ Input Matrix, $X$ State Vector, $u$ input vector, and Process noise $Q$, as well as general parameters like our time step $dt$ and physical parameters of our vehicle like mass and rotational inertia. The Emission Matrix $C$ is also generated here, with corresponding sensor noises $\sigma$.

%% Model parameters 
clear all
close all
dt = 0.1;       %sec (time step size)
T = 200;        %sec (simulation run time)
mass = 10;      %kg 
rI = 1;  %rotational inertia in Nms^2/degrees
thrust = 10;     %Newtons of force per thruster
t_rad = 0.2;    %meters from center thrusters mounted
 
goal = [10;14];     %meters x,y goal coordinates
cP = diag([1,1]);         %proportion control parameter dist,angle
cD = diag([.05,1]);        %derivative control parameter
%cI = 0;         %no buoyancy or anything to cause steady-state errors, so no intergral term
err = zeros(2,T/dt);    %distance and angle error
 
%initialize state
X = zeros(6,T/dt);         % [x y theta dx dy dtheta ]'
 
%create dynamics model - .98^10 drag / sec
A = [1 0 0 .99*dt 0 0;...
     0 1 0 0 .99*dt 0;...
     0 0 1 0 0 .99*dt;...
     0 0 0 .98 0 0;...
     0 0 0 0 .98 0;...
     0 0 0 0 0 .98 ;];
 
%create input dynamics      %for x, y, and theta forces/torques
B = [dt^2/2/mass 0 0;...
     0 dt^2/2/mass 0;...
       0 0 dt^2/2/rI;...
         dt/mass 0 0;...
         0 dt/mass 0;...
           0 0 dt/rI;];
 
%vector of inputs - Left and Right thruster
u =  zeros(2,T/dt);        %[left; right] thrusters
 
%translates motor inputs to x,y,theta force/torque inputs = motor*u 
motor = [1 1; 0 0; -1 1];
 
%Helper function - rotate thruster force from intrinsic to global coordinates         
rr = @(theta)[cosd(theta) -sind(theta) 0; sind(theta) cosd(theta) 0; 0 0 1];          
%Force/Torque = (rr(theta)*motor*u)          
 
%Process noise
Q = thrust/10;  %std = +/-10% of max thrust
 
%% Sensors 
% position sensor for x,y and oreintation sensor for yaw
C = [1 0 0 0 0 0;...
     0 1 0 0 0 0;...
     0 0 1 0 0 0;];
 
%Sensor noise 
sigma = [1.2; 1.2; 4];  %std x,y,theta - meters, meters, degrees
 
%% Initialize Model Values:
%Original Estimate
X_est(1:6,1:T/dt) = 0;   %assume all states zero on start-up
 
%Covariance Matrix (confidence of state estimation
P(:,:,1) = 9999*eye(6);    %covariance matrix of state estimation
%Initialize Model Values:
X(3,1) = 100;   %random initial orientation

This was just necessary to produce those nice .gif files. Ignore this unless you have some weird interest in matlab graphing syntax.

%% Initialize graphics
close all
f1 = figure(1);
set(f1, 'Position', [0 0 1920/2 1080/2]);
 
sp1 = subplot(1,2,1);
hold on
tT = title(['Position at Time = ',num2str(dt),'sec']);
 
gT = plot(goal(1),goal(2),'k*','MarkerSize',50);
pT = scatter(X(1,1),X(2,1),'MarkerEdgeColor','k','MarkerEdgeAlpha',.4);
vT = line([X(1,1),X(1,1)+X(4,1)/dt],[X(2,1),X(2,1)+X(5,1)/dt],'Color','g');
oT = line([X(1,1),X(1,1)+cosd(X(3,1))/2],[X(2,1),X(2,1)+sind(X(3,1))/2],'Color','r');
 
pE = scatter(X_est(1,1),X_est(2,1),'+','MarkerEdgeColor','b','MarkerEdgeAlpha',.4);
vE = line([X_est(1,1),X_est(1,1)+X_est(4,1)/dt],[X_est(2,1),X_est(2,1)+X_est(5,1)/dt],'Color','y');
oE = line([X_est(1,1),X_est(1,1)+cosd(X_est(3,1))/2],[X_est(2,1),X_est(2,1)+sind(X_est(3,1))/2],'Color','m');
 
utext = text(-1.5+X(1,1),3.5+X(2,1),['L = ',num2str(u(1,1)),'N R = ',num2str(u(1,1)),'N']);   %disp thruster values
 
hold off
xlim(2*[-1 1]), ylim(3*[-1 1])
xlabel('X pos [m]'), ylabel('Y pos [m]')
 
sp2 = subplot(1,2,2);
covP = imagesc(sqrt([P(:,:,1);4*ones(1,6)]));
covT = title(['Scale Covariance']);
xlim(sp2,[.5 6.5]), ylim(sp2,[.5 6.5])
xlabel('X [m] Y [m] \theta [deg] dX [m] dY [m] d\theta [m] '), 
ylabel('X [m] Y [m] \theta [deg] dX [m] dY [m] d\theta [m] '),
colorbar
 
frame(1) = getframe(f1);
tic;

Here's the meat of what you're looking for - third codeblock down, the Kalman Update section

%% Model / Filter update loop
for k = 1:T/dt    

%% Control System
    %calculate error
    err(1,k+1) = sqrt(sum((goal-X_est([1,2],k)).^2));
    err(2,k+1) = atan2d(goal(2)-X_est(2,k),goal(1)-X_est(1,k)) - X_est(3,k);
    err(2,k+1) = -err(2,k+1);   %correct for handed-ness
    while(abs(err(2,k+1))>180)
        err(2,k+1) = err(2,k+1) - sign(err(2,k+1))*360;
    end
 
    %calculate desired forces based on error
    f_goal = cP*err(:,k+1) + cD*(err(:,k+1)-err(:,k))./dt;
    f_goal(1) = cosd(err(2,k))*f_goal(1);   %reduce goal for wrong-facing direction
    f_goal = f_goal.*dt;
 
    %how to fire thrusters for desired translation
    u_t = f_goal(1) * [1;1];
    u_r = f_goal(2) * [1;-1];
    %Combine thrusts to acomplish goals - limit each goal to 50% thrust to truncate demand.
    u(:,k) = sign(u_t).*min(abs(u_t),thrust/2) + sign(u_r).*min(abs(u_r),thrust/2); 

    %% Model Submarine/thrusters (Reality normally does this job)
    %calculate new state from last state
    X(:,k+1) = A*X(:,k) + B*(rr(X(3,k))*motor*u(:,k) + Q*randn(3,1));
 
    %correct rollover
    while(abs(X(3,k+1))>180)
        X(3,k+1) = X(3,k+1) - sign(X(3,k+1))*360;
    end
 
    %calculate new sensor measurements from new state
    Y(:,k+1) = C*X(:,k+1) + sigma.*randn(3,1);

    %% Run Kalman Filter
    %Estimate new state from last state estimate
    X_est(:,k+1) = A*X_est(:,k) + B*(rr(X_est(3,k))*motor*u(:,k));
    %Estimate confidence in new estimate - model process noise of inputs
    % through input matrix
    P(:,:,k+1) = A*P(:,:,k)*A' + B*diag([Q Q Q].^2)*B';
 
    %Sensors only check in every n seconds
    if((mod(k*dt,0.5)) == 0)
        %Calculate Kalman Gain
        K = (P(:,:,k+1)*C')/(C*P(:,:,k+1)*C' + diag(sigma.^2));
 
        %Resolve new estimate
        X_est(:,k+1) = X_est(:,k+1)+K*(Y(:,k+1) - C*X_est(:,k+1));
        %Resolve new covariance matrix for estimate
        P(:,:,k+1) = (eye(size(X_est,1))-K*C)*P(:,:,k+1);
    end
 
    %Correct rollover
    while(abs(X_est(5,k+1))>180)
        X_est(3,k+1) = X_est(3,k+1) - sign(X_est(3,k+1))*360;
    end

 %% Graphic update
    %figure(1)
    tT.String = ['Position at Time = ',num2str(k*dt+dt),'sec'];
 
    pT.XData = X(1,1:k+1); 
    pT.YData = X(2,1:k+1);
 
    vT.XData = [X(1,k+1),X(1,k+1)+X(4,k+1)/dt]; 
    vT.YData = [X(2,k+1),X(2,k+1)+X(5,k+1)/dt];
 
    oT.XData = [X(1,k+1),X(1,k+1)+cosd(X(3,k+1))/2];
    oT.YData = [X(2,k+1),X(2,k+1)+sind(X(3,k+1))/2];
 
    pE.XData = X_est(1,1:k+1); 
    pE.YData = X_est(2,1:k+1);
 
    vE.XData = [X_est(1,k+1),X_est(1,k+1)+X_est(4,k+1)/dt]; 
    vE.YData = [X_est(2,k+1),X_est(2,k+1)+X_est(5,k+1)/dt];
 
    oE.XData = [X_est(1,k+1),X_est(1,k+1)+cosd(X_est(3,k+1))/2];
    oE.YData = [X_est(2,k+1),X_est(2,k+1)+sind(X_est(3,k+1))/2];
 
    utext.Position = [-1.5 3.5]+[X(1,k+1),X(2,k+1)];
    utext.String = ['L = ',num2str(u(1,k)),'N R = ',num2str(u(2,k)),'N'];
 
    xlim(sp1,X(1,k+1)+2*[-1 1]), ylim(sp1,X(2,k+1)+3*[-1, 1])
 
    covP.CData = sqrt([diag(1./[sigma; dt*sigma])*P(:,:,k+1)*diag(1./[sigma; dt*sigma]);4*ones(1,6)]);
 
    pause(dt/2-toc)
    tic;
 
    frame(ceil(k/2)+1) = getframe(f1);

That's the entirety of the update loop. It will stop when Time T/dt runs out or it hits an arbitrary stop condition

 %% Stop condition - close to target 
    if(sum(abs(goal-X_est(1:2,k+1))) < .3)
        break;
    end
 
end  %ends for k=1:T/dt loop

Why are you reading this? It's uninteresting.

%% clean up chart, close out and create gif
delete(utext);
for n=1:10
frame(ceil(k/2)+1+n) = getframe(f1);
end
xlim(sp1,[-5 20]), ylim(sp1,[-7.5 30])
for n=1:10
frame(ceil(k/2)+11+n) = getframe(f1);
end
movie2gif(frame, 'kalman_sim_halfs.gif', 'DelayTime', dt,'Loopcount',inf)
 
%%%End Program%%%