User Tools
Table of Contents
Sensors
Note: This section is currently under revision.
Sensors produce measurements that reflect the state of the external world - plus some noise. This section will go through what various sensors are measuring, their sources of noise, and how to relate them to states we want to keep track of.
Towards the end, a large example Emission Matrix will be given that demonstrates how to integrate several sensors into a Kalman Filter.
Accelerometer
An Accelerator measures acceleration. It's traducer is tantamount to a heavy mass in a box, connected to each wall by a spring. As the box gets accelerated from a direction, the mass's inertia resists, so the spring on one side is compressed, and the spring on the other is expanded. By measuring this contraction/expansion, the acceleration is estimated.
Modern microchip accelerometers are thin pieces of silicon, produced with similar fabrication techniques as microprocessors. The motion of the silicon chip is measured by changing the distance in several capacitors, which measurably alters the capacitance. However, the simpler mass-spring conceptualization is easier to talk about, so we'll stick with that.
The accelerometer feels all forces. This include gravity. If you push on a box, the mass will [relatively speaking] move in the opposite direction of acceleration. However, if you place the box on a table, gravity will cause it to sag, compressing the bottom spring and extending the top spring. The accelerometer will interpret it as being pushed upwards, not downwards. As such, we can see that body forces, like gravity, are not actually felt by the accelerometer. Only normal forces generated in response to them.
All together, an accelerometer feels 4 different forces. Gravity, Centripetal Acceleration, Rotational Acceleration, and Translational Acceleration.
$$ A = a_t + a_r + a_c + a_g $$
Gravity
The accelerometer feels all forces. This include gravity. If you push on a box, the mass will [relatively speaking] move in the opposite direction of acceleration. However, if you place the box on a table, gravity will cause it to sag, compressing the bottom spring and extending the top spring. The accelerometer will interpret it as being pushed upwards, not downwards. As such, we can see that body forces, like gravity, are not actually felt by the accelerometer. Only normal forces generated in response to them.
We can safely assume that gravity is always pulling downwards, by definition. However, it will not always add a static acceleration vector along the positive z-axis, because our sensor does not stay level. In fact, measuring gravity gives you an indication of an external static vector. The measurement of this vector is affected by your orientation. Conversely, by measuring your relation to this vector, you can help determine your orientation.
It should be noted that, due to the other sources of acceleration, utilizing an accelerometer's measurements to define your z-axis is likely to be very noisy.
So sitting still at orientation $R(\psi,\phi,\theta) = R(0,0,0)$ the accelerometer would measure $[0,0,+g]$ for $g \approx 9.8\frac{m}{s^2}$. If pitched upwards at $45^o$, the gravity vector would be detected by the positive z and positive x axis at $45^o$. This transformation would be tantamount to a negative pitch forward by the gravity acceleration relative to the accelerometer. As such, the Inverse Rotation Matrix $R^{-1} = R'$ describes how the gravity vector is rotated due to the submarine's orientation.
$$ a_g = R^T \begin{bmatrix} 0 \\ 0 \\ g \end{bmatrix} = \begin{bmatrix} 0 & 0 & g \end{bmatrix} R $$
Centripetal Acceleration
The centripetal acceleration felt by the accelerometer is give by the equation $\frac{v^2}{r} = \omega r^2 = \dot{\theta}^2r$. In 3 dimensions, we need to consider how this force is felt from rotation about each axis.
We can consider an accelerometer aligned with the submarine's internal $x,y,z$ axis located at Position $[p_x,p_y,p_z] = p[1,1,0]$. A rotation of $\dot{\theta} = 0.5\frac{rad}{sec}$ about the z-axis (yaw) would constitute a rotational velocity. The radius $r = \sqrt{(x^2 + y^2)} = \sqrt{2}$. So the centripetal force $a_{c:yaw} = (0.5^2)(\sqrt{2}) = \frac{1}{4}\sqrt{2} = \sqrt{\frac{2}{2}} = 1\frac{m}{s^2}$.
We can also find that the z-position $pz$ of the submarine would not impact the centripetal acceleration felt by the accelerometer. This calculated value would hold for any $p[1,1,p_z]$.
However, how will this force be detected by the accelerometer? Centripetal Acceleration is another body force. It is accelerating all masses towards the outside - the accelerometer then feels the inward normal force created by the rigid structure it's attached to preventing it from moving in the face of the acceleration. So the acceleration vector measured will be negative, pointing back at the origin.
Furthermore, the acceleration felt will be broken up across sensors. Some proportion of it will be felt as negative acceleration along the x-axis, and some proportion along the y-axis. Consider instead if the accelerometer was at the position $p[\sqrt{2},0,0]$. The centripetal acceleration felt would be the same, but it would be measured entirely as a positive x component $a_{c:yaw} = [-\sqrt(2),0,0]$.
Were it at position $p[0,\sqrt{2},0]$ the entirety of the acceleration would be felt as a y componenet $a_{c:yaw} = [0,-\sqrt(2),0]$.
We can generalize the solution and calculate the centripetal force felt from roll, pitch, and yaw rotational velocity from an arbitrary $p[x,y,z]$ position.
The position does not influence the rotational velocity - all rotations are felt equally regardless of position on rigid bodies. This leaves the radius to be calculated. The radius $r = \sqrt{p_x^2 + p_y^2}$. The angle of this force acts on the accelerometer is also the angle formed from the center of rotation (origin) $\theta = \tan{\frac{p_y}{p_x}}$.
The math works out quite conveniently.
$$ r = \sqrt{p_x^2 + p_y^2}, \quad \theta = \arctan{\frac{p_y}{p_x}} \\ p_x = r\cos{\theta}, \quad p_y = r\sin{\theta} \\ a_x = \omega^2r\cos{\theta}, \quad a_y = \omega^2r\sin{\theta} \\ $$
Therefore:
$$ a_x = \omega^2p_y, \quad a_y = \omega^2p_x, \quad a_z = 0 $$
The trigonometric terms cancle out and the acceleation detected along each axis is proportional to the position along that axis. Therefore, we've calculated the a_c contribution from yaw. We can generalize this calculation to roll and pitch.
Yaw
$$ r = \sqrt{p_x^2 + p_y^2}, \quad \theta = \arctan{\frac{p_y}{p_x}} \\ p_x = r\cos{\theta}, \quad p_y = r\sin{\theta} \\ a_x = -\omega^2r\cos{\theta}, \quad a_y = -\omega^2r\sin{\theta} \\ a_x = -p_x * \omega^2, \quad a_y = -p_y * \omega^2, \quad a_z = 0 $$
Pitch
$$ r = \sqrt{p_x^2 + p_z^2}, \quad \theta = \arctan{\frac{p_z}{p_x}} \\ p_x = r\cos{\theta}, \quad p_z = r\sin{\theta} \\ a_x = \omega^2r\cos{\theta}, \quad a_z = \omega^2r\sin{\theta} \\ a_x = -p_x * \omega^2, \quad a_y = 0, \quad a_z = -p_z * \omega^2, \quad $$
Roll
$$ r = \sqrt{p_y^2 + p_z^2}, \quad \theta = \arctan{\frac{p_z}{p_x}} \\ p_y = r\cos{\theta}, \quad p_z = r\sin{\theta} \\ a_y = \omega^2r\cos{\theta}, \quad a_z = \omega^2r\sin{\theta} \\ a_x = 0, \quad a_y = -p_y * \omega^2, \quad a_z = -p_z * \omega^2, \quad $$
Total Summation
Putting this all together we get the total centripetal acceleration felt on an accelerometer at position $[p_x,p_y,p_z]$ with rotational velocities $\dot{R} = [\dot{\psi},\dot{\phi},\dot{\theta}]$.
$$ a_x = (0 * \dot{\psi}^2) + (-p_x * \dot{\phi}^2) + (-p_x * \dot{\theta}^2) \\ a_y = (-p_y * \dot{\psi}^2) + (0 * \dot{\phi}^2) + (-p_y * \dot{\theta}^2) \\ a_z = (-p_z * \dot{\psi}^2) + (-p_z * \dot{\phi}^2) + (0 * \dot{\theta}^2) \\ $$
Thus we can turn this into a matrix format and get:
$$ a_c = \begin{bmatrix} a_{cx} \\ a_{cy} \\ a_{cz} \end{bmatrix} = \begin{bmatrix} 0 & -p_x & -p_x \\ -p_y & 0 & -p_y \\ -p_z & -p_z & 0 \end{bmatrix} \begin{bmatrix} \dot{\psi}^2 \\ \dot{\phi}^2 \\ \dot{\theta}^2 \\ \end{bmatrix} $$
Finally, it's worth noting that because the accelerations felt are a function of rotational velocity squared, the direction of rotation is irrelevant. The force felt is inwards, and favors neither direction. We know this about centripetal force intuitively, but it's nice to see math reflected our common-sense.
Translational and Rotational Acceleration
The Translational and Rotational Accelerations are both felt as individual point-accelerations. Rotational Acceleration only makes sense as the difference of accelerations felt on two parts of a rigid body. The translational acceleration of the body is the average of these accelerations.
Assume two accelerometers are placed at locations $p_1[1,0,0]$ and $p_2[-1,0,0]$. An acceleration of $1\frac{m}{s^2}$ along the x-axis would be measured as $a_1[1,0,0]$ and $a_2[1,0,0]$. They would be felt equally. A yaw acceleration $\alpha_{yaw}=\frac{a}{r} = 1\frac{rad}{sec^2}$ about the origin would be felt as a sideways acceleration on each accelerometer. The forward accelerometer would be accelerated to the left, into the positive y-axis. The back accelerometer would be accelerated in the opposite direction, into the negative y-axis. Thus the accelerations felt would be $a_1[0,1,0]$ and $a_2[0,-1,0]$. They would experience opposite accelerations.
$$ a_t = \frac{a_1 + a_2}{2},\quad a_r = \frac{a_1 - a_2}{2} $$
It should also be noted, that this math describes the translational acceleration felt by the center of rotation. That is defined as the origin, or center of mass, for convenience. But it can technically be defined as any arbitrary set of coordinates. Demonstrating that is an exercise left to the student.
However, this only works for two accelerometers placed along a common axis at equal distances. We want generalized equations for arbitrary accelerometer placement.
Consider if the two accelerometers were instead placed at $p_1[0,1,0]$ and $p_2[0,-1,0]$ and subjected to the same translational acceleration $a_t=[1,0,0]$. The translational accelerations felt would be equal to the first case. Translational acceleration is felt universally on the rigid body. Subjected to the same rotational acceleration of $\alpha_{yaw} = 1\frac{rad}{sec^2}$, however, the left accelerometr would be accelerated backwards toward the negative x-axis, with $a_1[-1,0,0]$ and the right accelerometer would feel an opposite acceleration forward $a_2[1,0,0]$. Were the acceleration doubled to $\ddot{\theta} = 2\frac{rad}{sec^2}$, the accelerations felt would be equal to $[-2,0,0]$ and $[2,0,0]$.
Like in the centripetal acceleration case, the z-axis position does not affect the rotational forces felt by a yaw acceleration. Using trigonometry, we can find the calculations for acceleration components felt from a given yaw acceleration at an arbitrary point. Again, like with the centripetal force, the rotational force components will depend will depend on angle $\theta = \tan{\frac{p_y}{p_x}}$. The difference is the acceleration felt will be orthogonal to that vector, rather than lie alongside it.
$$ p = [p_x,p_y,p_z], \quad \alpha = \frac{a}{r} \\ r = \sqrt{p_x^2 + p_y^2}, \quad \theta = \arctan{\frac{p_y}{p_x}} \\ p_x = r\cos{\theta}, \quad p_y = r\sin{\theta} \\ a_x = -\alpha * r\sin{\theta}, \quad a_y = \alpha * r\cos{\theta} \\ a_x = -p_y * \alpha, \quad a_y = p_x * \alpha, \quad a_z = 0 $$
Note that the acceleration vector is felt orthogonal to the position of the accelerometer. Thus, the rotational acceleration vector felt from a yaw acceleration is equal to the position vector $[p_x,p_y,p_z]$ crossed with the z-axis $[0,0,1]$, scaled by the actual yaw acceleration about the z-axis. This is why we get the p_x term for the y component, but a negative p_y term for the x component, and a 0 along the z-axis.
We can take this method of finding the acceleration vector and apply it to pitch and roll accelerations, to find the total rotational acceleration felt.
Yaw
$$ p = [p_x,p_y,p_z], \quad \alpha = \frac{a}{r} \\ r = \sqrt{p_x^2 + p_y^2}, \quad \theta = \arctan{\frac{p_y}{p_x}} \\ p_x = r\cos{\theta}, \quad p_y = r\sin{\theta} \\ a_x = -\alpha * r\sin{\theta}, \quad a_y = -\alpha * r\cos{\theta} \\ a_x = -p_y * \alpha, \quad a_y = p_x * \alpha, \quad a_z = 0 $$
Pitch
$$ p = [p_x,p_y,p_z], \quad \alpha = \frac{a}{r} \\ r = \sqrt{p_x^2 + p_z^2}, \quad \theta = \arctan{\frac{p_z}{p_x}} \\ p_x = r\cos{\theta}, \quad p_z = r\sin{\theta} \\ a_x = \alpha * r\sin{\theta}, \quad a_z = -\alpha * r\cos{\theta} \\ a_x = p_z * \alpha, \quad a_y = 0, \quad a_z = -p_x * \alpha, \quad $$
Roll
$$ p = [p_x,p_y,p_z], \quad \alpha = \frac{a}{r} \\ r = \sqrt{p_y^2 + p_z^2}, \quad \theta = \arctan{\frac{p_z}{p_y}} \\ p_y = r\cos{\theta}, \quad p_z = r\sin{\theta} \\ a_y = -\alpha * r\sin{\theta}, \quad a_z = \alpha * r\cos{\theta} \\ a_x = 0, \quad a_y = -p_z * \alpha, \quad a_z = p_y * \alpha, $$
Total Summation
Putting this all together we get the total acceleration felt on an accelerometer at position $[p_x,p_y,p_z]$ with rotational acceleration $\dot{R} = [\ddot{\psi},\ddot{\phi},\ddot{\theta}]$.
$$ a_x = (0 * \ddot{\psi}) + (p_z * \ddot{\phi}) + (-p_y * \ddot{\theta}) \\ a_y = (-p_z * \ddot{\psi}) + (0 * \ddot{\phi}) + (p_x * \ddot{\theta}) \\ a_z = (p_y * \ddot{\psi}) + (-p_x * \ddot{\phi}) + (0 * \ddot{\theta}) \\ $$
Whatever value remains after the rotational components have been removed is the true translational acceleration $a_t$. Thus we can turn this into a matrix format and get:
$$ a = a_t + a_r = \begin{bmatrix} a_{x} \\ a_{y} \\ a_{z} \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 & p_z & -p_y \\ 0 & 1 & 0 & -p_z & 0 & p_x \\ 0 & 0 & 1 & p_y & -p_x & 0 \end{bmatrix} \begin{bmatrix} \ddot{x} \\ \ddot{y} \\ \ddot{z} \\ \ddot{\psi} \\ \ddot{\phi} \\ \ddot{\theta} \\ \end{bmatrix} $$
As we can see, there are six state variables, and we only have a vector of 3 measurements from one accelerometer. Thus the math reflects the realistic constraints - we need at least two accelerometers to separate rotational and translational acceleration components.
Total Matrix
We can combine everything now to express the entirety of what our accelerometer measures as a function of our state variables.
$$ A = (a_t + a_r) + a_c + gR \\ A = \begin{bmatrix} 1 & 0 & 0 & 0 & p_z & -p_y \\ 0 & 1 & 0 & -p_z & 0 & p_x \\ 0 & 0 & 1 & p_y & -p_x & 0 \end{bmatrix} \begin{bmatrix} \ddot{x} \\ \ddot{y} \\ \ddot{z} \\ \ddot{\psi} \\ \ddot{\phi} \\ \ddot{\theta} \end{bmatrix} + \begin{bmatrix} 0 & -p_x & -p_x \\ -p_y & 0 & -p_y \\ -p_z & -p_z & 0 \end{bmatrix} \begin{bmatrix} \dot{\psi}^2 \\ \dot{\phi}^2 \\ \dot{\theta}^2 \end{bmatrix} + \begin{bmatrix} 0 & 0 & g \end{bmatrix} \begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix} $$
Condensing all states into one vector, we get the overall matrix:
$$ \begin{bmatrix} 1 & 0 & 0 & 0 & p_z & -p_y & 0 & -p_x & -p_x & 0 & 0 & 0 & 0 & 0 & 0 & g & 0 & 0 \\ 0 & 1 & 0 & -p_z & 0 & p_x & -p_y & 0 & -p_y & 0 & 0 & 0 & 0 & 0 & 0 & 0 & g & 0 \\ 0 & 0 & 1 & p_y & -p_x & 0 & -p_z & -p_z & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & g \end{bmatrix} \begin{bmatrix} \ddot{x} \\ \ddot{y} \\ \ddot{z} \\ \ddot{\psi} \\ \ddot{\phi} \\ \ddot{\theta} \\ \dot{\psi}^2 \\ \dot{\phi}^2 \\ \dot{\theta}^2 \\ R_{11} \\ R_{12} \\ R_{13} \\ R_{21} \\ R_{22} \\ R_{23} \\ R_{31} \\ R_{32} \\ R_{33} \end{bmatrix} $$
This seems like quite an excessively rectangular matrix to be using. However, other sensors will also utilize some of these states. Thus, this form is preferable, as we can easily integrate it with other sensors simply by expanding the rows of the left matrix.
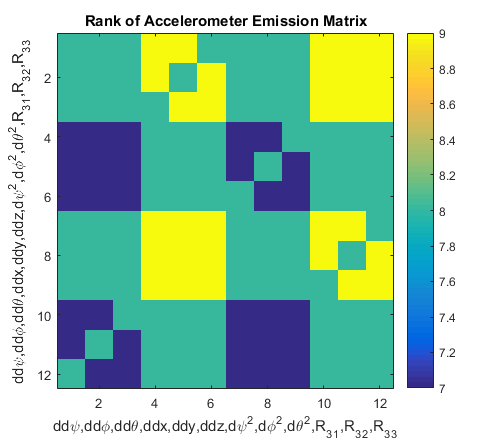
Sensor Emission Matrix Rank
We can also look at our matrix and learn something about what kind of information we need. There are 18 state variables.
6 of them - elements from the 3×3 rotation matrix $R$ - do not interact with our accelerometer at all - which means that accelerometers alone, no matter how many, cannot tell us our orientation. They can tell us, however, the rotation matrix elements $R_{31},R_{32},R{33}$ which make up the bottom row of the rotation matrix. If you check the 3D Rotation Section in the wiki, you can see that these three pieces of information alone can inform us of our pitch and roll. They can tell us nothing about the yaw of the submarine, which makes perfect sense as detecting a downward pointing gravity vector will never tell us anything about our heading.
Beyond that, there are 9 other values. Naively, we might conclude that with 4 accelerometers placed at four separate locations, we could fully determine the translational acceleration, rotational acceleration, square of the rotational velocity, and the tilt (pitch/roll) of the submarine. All 12 total states.
However, if we use 4 random locations $p_1,p_2,p_3,p_4$ to construct the matrix, and find its rank, it evaluates to $9$. Not $12$. It is important the positions be random, so that symmetry does not cheat us out of any information. It may also be worth investigating accelerometers placed precisely at the origin, and unit vectors along each axis, to see if there's any theoretical information available, but realistic constraints prevent us from every placing accelerometers so precisely.
Thus, there are only 9 of those values that can be determined from accelerometers alone. To find which states are linked, we can systematically remove columns from the matrix and re-test its rank. If the rank diminishes, then that column was an independent vector and corresponds to a state not ineffably tied to the value of any other state.
By removing up to two columns at a time, we can find any pair of columns that are mutually dependent. The first and third collection of three columns are both clearly independent, as removing any one of them diminishes the rank by 1, and removing any 2 diminishes the rank by 2. They correspond to the rotational and centripetal accelerations. That leaves the rotation matrix elements, and the translational accelerations as co-dependent.
This makes sense, as an object can not tell the difference between [normal forces opposing] gravity and acceleration. Rotational and centripetal accelerations can be cessed out because they are felt differently based on position. Translational acceleration and gravity are felt equally and universally.
Anyway, as this shows, we need some other information from another sensor to fix the values of either the translational accelerations, or the pitch and roll of the system, in order for us to estimate the other state variables. It also shows that we need only 3 3-axis accelerometers to collect all unique data. Anything beyond this will just provide redundant information that reduces noise - helpful, but not vital. The Kalman filter allows us to make estimations of all states absent other measurements, since it uses the forward-predicted values of the states as additional pseudo-measurements, which in and of itself is a full-rank 'measurement'. However, those measurements will not be very accurate. Accelerometers should be augmented with more sensors.
Gyroscopes
Gyroscopes are nice and simple. They measure the rotational velocity about an axis. 3 together provide you with a direct measurement of your roll, pitch, and yaw velocities $\dot{\psi},\dot{\phi},\dot{\theta}$. Rotational velocity is felt equally in all placed on a rigid body, so placement of the gyroscopes does not factor in (though proper alignment with the $x,y,z$ axes of the submarine's intrinsic coordinate system is necessary).
Gyroscopes are, however, subject to drift. As they operate, the velocity will have some offset. As a function of temperature and time, this offset value will slowly change. Over short instances it is not problematic - the estimates of angular acceleration $\ddot{\psi},\ddot{\phi},\ddot{\theta}$ the Kalman Filter will generate based off gyroscope measurements will be very accurate. However, the rotational velocity itself is an important measurement and should be accounted for.
$$ G = \begin{bmatrix} G_{\dot{\psi}} \\ G_{\dot{\phi}} \\ G_{\dot{\theta}} \\ \end{bmatrix} = \begin{bmatrix} \dot{\psi} \\ \dot{\phi} \\ \dot{\theta} \\ \end{bmatrix} + \begin{bmatrix} err_{\dot{\psi}} \\ err_{\dot{\phi}} \\ err_{\dot{\theta}} \\ \end{bmatrix} $$
This presents a problem. We have two unknown values - the true velocity measurement, and the offset, for every one piece of information - the Gyroscope measurement.
Thus the system must be calibrated. On Start-up, we need to externally fix the rotational speed of the submarine to $[\dot{\psi},\dot{\phi},\dot{\theta}] = [0,0,0]$ and then take a measurement of what remains. That will be the offset values.
This is generally sufficient. However, submarine missions will run for long periods of time. Competition runs take up to 20 minutes, and pool tests see the submarine in the water for potentially hours at a time. The next section covers how to set-up something better, if desired.
Error Tracking
A possible solution is to have the system itself track the offset of each axis of each gyroscope as an extra state variable. Mathematically, the set-up would look like this:
$$ \begin{bmatrix} 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \dot{\psi} \\ \dot{\phi} \\ \dot{\theta} \\ err_{\dot{\psi}} \\ err_{\dot{\phi}} \\ err_{\dot{\theta}} \\ \end{bmatrix} = \begin{bmatrix} G_{\dot{\psi}} \\ G_{\dot{\phi}} \\ G_{\dot{\theta}} \\ \end{bmatrix} $$
Obviously, this will have trouble working on its own. We have 6 unknown values and only 3 measurements. However, let's see what happens when we use an additional gyroscope.
$$ \begin{bmatrix} 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \dot{\psi} \\ \dot{\phi} \\ \dot{\theta} \\ err_{1\dot{\psi}} \\ err_{1\dot{\phi}} \\ err_{1\dot{\theta}} \\ err_{2\dot{\psi}} \\ err_{2\dot{\phi}} \\ err_{2\dot{\theta}} \\ \end{bmatrix} = \begin{bmatrix} G_{1\dot{\psi}} \\ G_{1\dot{\phi}} \\ G_{1\dot{\theta}} \\ G_{2\dot{\psi}} \\ G_{2\dot{\phi}} \\ G_{2\dot{\theta}} \\ \end{bmatrix} $$
This is better. Now we have 9 unknowns and 6 measurements. However, no matter how many gyroscopes we add, we will always be 3 measurements short. We need some prime gyroscope with no error to definitively fix the rotational rates, after which the remaining gyroscopes could be used to solve for their own errors.
This doesn't really seem to help us at all. We wouldn't need to track offset errors if we could make a perfect gyroscope. Alone, gyroscopes cannot track their own error.
However, we're not alone. We've got other sensors, and a Kalman Filter. The Kalman Filter provides predicted locations as state variable measurements based on previous states. And the Kalman Filter's states are informed by multiple sensors, including absolute orientation information obtained from magnetometers, accelerometers, and depth sensors, among other things.
Thus, through the Kalman Filter, the sensors describing orientation will also estimate the derivative of orientation - the rotational velocity. If a magnetometer continues to point in the same direction while a gyroscope insists the submarine is yawing at $5^o/sec$, the Kalman Filter will resolve the two, estimate a velocity of $2.5^o/sec$ and an orientation to match. The gyroscope's drift will be estimated to be $+2.5^o/sec$. On the next measurement 1 second later, the magnetometer will indicate a heading of $-2.5^o$ and suggest a yaw velocity of $-2.5^o/sec$ while the gyroscope, will assert a rotational velocity of $2.5^o/sec$, after subtracting its offset. The Kalman Filter will again resolve this, and estimate a gyroscopic drift closer to $5^o/sec$, after which the gyroscope and magnetometer should continue to be in agreement until significant drift accumulates in the gyroscope again.
In reality, it is not quite as clean as the above example. In that example, the derivative measurement of the magnetometer was assumed to be absolutely correct, and the gyroscope did not resist its drift changing by several degrees in a few seconds. Gyroscopes do not drift that quickly, and the offset should know and assert that. Meanwhile, magnetometers will also be noisy, and jump around within a certain range, so their noise will inform the system not to trust it - or derivatives derived from its changes between time-steps, to be fully trusted. The Kalman Filter properly informed will still slowly adjust the drift until the gyroscope and magnetometer converge at some point, but it will do so according to the weight given to the two sensors and the offset based off of noise.
As part of the Process noise, the gyroscope's offsets must be given their own value which indicates it's likelihood to drift over time. This value will come into conflict with the error measured between the noisy gyroscope and magnetometer. Too high of a process noise, and all disagreements between the two sensors will just be attributed to a rapidly changing offset error, and the actual gyroscope measurements will not contribute to the state estimation. Too low of a Process Noise, and the gyroscope will stubbornly believe itself over the magnetometer (or other orientation sensors) and force the Filter to estimate significantly deflected headings as rotational. Finding a proper balance between the weights given to the magnetometer, gyroscope, and offset drift noise is the key to resolving this issue.
If it can be resolved, however, you will have a gyroscopic system that does not need calibration on start-up, nor suffer from drift during long operation. It should be stated however, that calibration is always good to perform when possible. Introducing a temporary 'calibration sensor' that asserts rotational velocity to be 0 with ~0 variance will force the gyroscopes to set their offsets to the current value no matter what.
Magnetometer
Depth Sensor
A Depth Sensor is a pressure traducer that measures pressure (and sometimes temperature) and determines the depth of water sitting atop it. They tend to be very accurate and reliable.
If somebody wants to work out the math for the minute corrections for pressure added or subtracted based on depth sensor orientation and velocity, they're free too.
The absolute depth (z-position) of the submarine has to describe a single point - typically the submarine's center of mass. This point also serves as the origin for the Submarine's intrinsic coordinate system.
A depth sensor placed arbitrarily on the submarine will measure it's own depth, which will be the depth of the submarine, plus the z-component of it's position. Failing to account for this will result in the control system balancing the depth of the sensor, and not the submarine itself.
Additionally, if the submarine pitches or rolls, the z-offset is altered. A depth sensor placed at $[-0.5,0,0]$ will offer the depth of the submarine without adjustment, however, were the submarine to pitch upwards by $90^o$, the control system would hold the depth sensor at a fixed depth, and the true submarine would rise to half a meter above its desired depth.
Therefore, we must account for the absolute position of the submarine, the depth sensors position relative to the submarine, and the orientation of the submarine.
$$ Depth_{xyz} = Sub_{xyz} + R(\psi,\phi,\theta) * pos_{xyz} \\ D = \begin{bmatrix} D_x \\ D_y \\ D_z \\ \end{bmatrix} = \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} + \begin{bmatrix} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{bmatrix} \begin{bmatrix} p_x \\ p_y \\ p_z \\ \end{bmatrix} $$
We can take the transpose of this equation and reorganize this to be an equation with a single term:
$$ \begin{bmatrix} p_x & p_y & p_z & 1 \\ \end{bmatrix} \begin{bmatrix} R_{11} & R_{21} & R_{31} \\ R_{12} & R_{22} & R_{32} \\ R_{13} & R_{23} & R_{33} \\ x & y & z \end{bmatrix} = \begin{bmatrix} D_x & D_y & D_z \end{bmatrix} $$
Unfortunately for us, depth sensors tell us their absolute z position $D_z$, but they have no way to know $D_x$ or $D_y$. So our measurement is a single scalar value $D_z$. Meaning the first two columns of that state-matrix are irrelevant.
$$ \begin{bmatrix} p_x & p_y & p_z & 1 \\ \end{bmatrix} \begin{bmatrix} R_{31} \\ R_{32} \\ R_{33} \\ z \end{bmatrix} = \begin{bmatrix} D_z \end{bmatrix} $$
Here we have 4 unknowns and 1 measurement. If we know the bottom row of the $R$ Matrix (ie. know our pitch and roll) we can calculate the submarine's depth from there. However, it is clear that we can make the left emission matrix full-rank with proper choice of depth sensor positions. Were we to use 4 or more depth sensors, we could fully determine our roll, pitch, and depth. It would help our accelerometers separate out gravity from its translational acceleration, for instance.
Why do we need 4 depth sensors and not 3? Consider any 3 depth sensors. Their positions would define some sort of plane. Were the submarine to rotate to an orientation where that plane was level with the external $x,y$ plane, the sensors would read equal depth values. If the submarine rolled over 180 degrees, the depth sensors would all be on the same plane again, and the submarine would have no way of differentiating between the two cases. A 4th depth sensor not co-planar to the other three must be added. It will then be above, or below the other three sensors in each case, removing ambiguity.
Thus, to make the emission matrix full-rank, we need at least 4 non-co-planar depth sensors.
$$ \begin{bmatrix} p_{1x} & p_{1y} & p_{1z} & 1 \\ p_{2x} & p_{2y} & p_{2z} & 1 \\ p_{3x} & p_{3y} & p_{3z} & 1 \\ p_{4x} & p_{4y} & p_{4z} & 1 \end{bmatrix} \begin{bmatrix} R_{31} \\ R_{32} \\ R_{33} \\ z \end{bmatrix} = \begin{bmatrix} D_{1z} \\ D_{2z} \\ D_{3z} \\ D_{4z} \\ \end{bmatrix} $$